Adaptive Median Filter for Image Corrupted by Salt and Pepper Noise

The image denoising is a preprocessing step in image processing and is used to recover the image which is corrupted by noise. It shown below the image corrupted by impulsive noise or salt and pepper noise is denoised by Adaptive Median filter.

Impulsive noise is added to an image when the image is transmitted over a noisy channel and decoding error on the receiver side. It is modelled by imnoise function in Matlab programming.

Median filter with small fixed window size is a preferred technique for denoising an image corrupted by salt & pepper noise because of simple and efficient. However, it is performance decreased the image corrupted by high density noise pixels.

Adaptive Median filter changing it's window size depends on density of noise is a preferred technique for denoising an image corrupted by high density salt & pepper noise.

Original Image and 70% salt & pepper noised image
Denoised image by Adaptive median filter

Adaptive Median Filter - Algorithm steps

• set ws=3, wsmax =21
• m,n - row and column index of noised image
• read neighbouring-pixels w.r.t m,n and ws
• Find S1,S2 and S3
  • S1 = min(neighbouring-pixels)
  • S2 = median(neighbouring-pixels)
  • S3 = max(neighbouring-pixels)
• IF IS-ASCENDING[S1,S2,S3] AND S1 >pixel(m,n)< S3 THEN
  • pixel(m,n) not corrupted
  • ELSE pixel(m,n) replaced by S2
• ELSE
  • increment ws by 2
  • IF ws > wsmax THEN break

Matlab programming - Adaptive Median Filter

 
function adaptwindsp
%adaptive median filter  salt pepper denoising  
clc; clear all;
close all;

% read an image from a file and store their intensity in a 2D matrix, im
fname= 'cameraman.tif';
[im,map] = imread(fname);
%find number of rows and columns in the image
[N,M]=size(im);

% percentage of noise (salt & pepper)  to add into the input image 
noisep =70/100; 
nim=imnoise(im,'salt & pepper',noisep);

% initialize denoised image matrix with zeros elements
dim=zeros(M,N);

% set maximum median filter window size
wsmax=21; 

for m=1 : M
  for n=1 : N  

    % set minimum median filter window size
    ws =3; 
    while ( ws < wsmax )
     
      %  neighbouring subscripts of centre pixel           
     hws = floor(ws/2);
     [J,I]=meshgrid(n-hws:n+hws ,m-hws:m+hws);
     I=I(:); J=J(:);          

      % exclude subscripts out of border of the image 
      if ( m<=hws || n<=hws || m>=M-hws || n>=N-hws)        
            s =(I>=1 & I<=M);
            I=I(s); J=J(s);      
            s =(J>=1 & J<=M);
            I=I(s); J=J(s);       
      end      

     %  converts neighbouring subscripts index  
      ind = sub2ind([M,N],I,J);          
       
     %  minimum of neighbouring pixels  
      S1 = min ( nim(ind)  ) ;
     %  median of neighbouring pixels  
      S2 =  median ( nim(ind)  );
     %  maximum of neighbouring pixels  
      S3 =  max( nim(ind) );
       
       if ( S1<S2 && S2<S3 )
           
           if ( nim(m,n)>S1 && nim(m,n)<S3 ) 
                 dim(m,n) = nim(m,n);                
           else
                dim(m,n) = S2; 
           end
           break;
           
       else  
           % increment  median filter window size by 2         
           ws = ws+2;           

            %  if max window size reached, set S2 as denoised pixel and 
              % break the while-loop          
           if (  ws > wsmax )
                  dim(m,n) = S2;
                  break;
           end           
       end
             
    end
  end
end

% display input image &  noised (salt & pepper) image   
figure;subplot(1,2,1);imshow(im,map); title('Input image');
subplot(1,2,2);imshow(nim,map);  
title( sprintf( 'salt & pepper noised image : %.1f%',noisep*100));


L=M*N;  dim=uint8(dim);
% sum absolute difference between original and denoised  image
mae=(1/L)* sum(sum( abs(im-dim) ));
%  mean square error between original and denoised  image
mse=(1/L)* sum(sum((im-dim).^2));
%  peak to signal ratio between original and denoised  image
psnr=20.0* (log10(255/sqrt(mse)));

% display   noised (salt & pepper) image and denoised image 
  % by adaptive median filter  
figure;subplot(1,2,1);imshow(nim,map);
title( sprintf( 'salt & pepper noised image : %.1f%',noisep*100));
subplot(1,2,2);imshow(dim,map);
title( sprintf( 'Denoised  Image : %.2f db', psnr ));

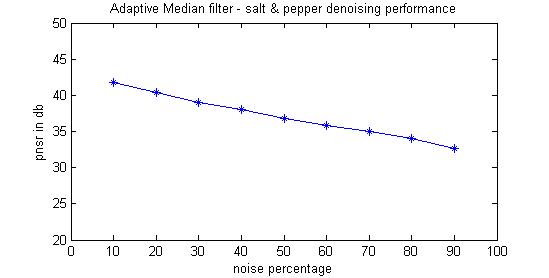
Adaptive Median Filter Image Denoising - Experiments & results

Input image size : 256 x 256 
salt & pepper noise percentage : 70.0 
mean absolute error : 3.54
mean square error : 20.70
psnr : 34.97

90% salt & pepper noised image and Reconstructed image

Adaptive Median Filter performance graph - noise-level vs psnr